Astronoomid mängivad digitaalse plastiliiniga juba ammu

Mida kiiremini omandavad astronoomid uued masinõppe tehnoloogiad, seda kaugemale ja detailsemalt hakkab inimene koos masinatega maailmaruumi nägema.

JAAN PELT

Hamburgi observatoorium asub Bergedorfi äärelinnas ja on ümbritsetud kena rohelise pargiga. Pargis on Eestist pärit teleskoobiehitaja Bernhard Schmidti väike muuseum ja sealt võib leida ka hulganisti viljapuid. Minu võõrustaja, norra-saksa astronoom Sjur Refsdal näitas mulle kohe saabumisel, millised pirnipuud on talle eraldatud, ja soovitas lahkelt pirne süüa, kui isu on. Seda ei pidanud kaks korda ütlema, eriti kui silmas pidada, kui vaene aeg oli 1990ndate algus eestlaste jaoks.

Pirne oli palju. Kui ma ütlen palju, siis lugeja saab enamasti aru, kui palju on „palju“. Mingisugune ettekujutus tekib inimestel ka siis, kui öelda, et Linnu­tees (meie kodugalaktikas) on umbes 100 miljardit tähte. Oleme harjunud ka teadmisega, et maa peal elab üle 8 miljardi inimese. Kui aga räägime tähtede koguarvust vaadeldavas universumis (umbes 200 000 000 000 000 000 000 000), siis on meie ettekujutusvõime juba tõsises hädas. Kuid see pole veel kõik – tähtede heledus ja muud omadused võivad ajas kiiresti muutuda. Seega tuleks kogu seda suurt hulka vaadelda enam-vähem pidevalt muutuva pildireana.

Traditsioonilises astronoomias vaatles üks vaatleja teleskoobiga ühte tähte. Teda võis aidata assistent, kes kirjutas üles, mida observaator nägi. Sellisel kombel avastas näiteks Friedrich Georg Wilhelm Struve Tartu tähetornis Veega-nimelise tähe asukoha väikese muudatuse ja sai selle põhjal arvutada, esimesena maailmas, tähe kauguse meist.

Väga olulise muutuse astronoomide töösse tõi fotograafia kasutuselevõtt. Näiteks võiks olla 1950. aastatel teostatud esimene Palomari taevauuring. Taeva süstemaatiliseks pildistamiseks kasutati Lõuna-Californias Palomari mäel asuvat 48tollist Oschini teleskoopi. See Bernhard Schmidti leiutatud optilise skeemiga teleskoop võimaldas koguda üle 2000 suure lahutusvõimega foto, mis katsid kogu vaatluspaigas kättesaadava taevaala. Plaatide kogu teisendati hiljem digitaalsesse vormingusse ja on ka praegu internetis hõlpsasti juurdepääsetav.

Huvitav on see, et Eesti astronoomidel õnnestus sügaval Nõukogude ajal välja kaubelda raha plaatide negatiividest tehtud fotode ostmiseks. Tõraveres asuva observatooriumi toonane ase­direktor Charles Villmann oli suutnud veenda Moskva otsustajaid, et tegemist on tulusa tehinguga – iga galaktika eest tuli maksta ainult 0,01 Ameerika senti!

Eriti usinad Palomari fotode kasutajad olid Tõravere astronoomid Mihkel Jõeveer ja Erik Tago Jaan Einasto töörühmast. Tulemused on meile hästi teada.

Palomari piltide juurde tuleme allpool tagasi.

Ülikauged tähed

Läbi galaktikateparve MACS J1149.6+2223 paistnud supernoova SN Refsdal¹ uurimisel tehti Hubble’i teleskoobiga huvitav avastus.

Täiesti juhuslikult leiti 29. aprillil 2016. aastal tehtud pildilt täpike, mille heledus oli võrreldes eelmiste piltidega tugevalt kasvanud. Patrick L. Kelly juhitud meeskond püüdis aru saada, mis juhtus. Pärast kõigi hüpoteeside kontrollimist leidsid nad vastuse – tegemist on tähega! Avastatud täht, mis sai endale ilusa nime Icarus, oli kõigist seni vaadeldud tähtedest umbes 100 korda kaugemal.

Muidugi teati, et kaugel galaktikas asuva tähe valgust võib olla võimendanud ees olev gravitatsiooniline lääts, galaktikate parv. Selle teadaoleva võimenduse suurus aga oli ebapiisav tähekujutise tekkeks. Appi tuli võtta veel üks efekt, nn mikroläätse efekt, mida varem oli teoreetiliselt uurinud ka Sjur Refsdal. Tegemist on juhuga, kui maapealse vaatleja ja kauge tähe vahele tõmmatud vaatekiirele satub mõneks ajaks teine täht, mis asub ühes parve galaktikatest. Siis võib juhtuda, et kaugema tähe näiv heledus võib tugevalt kasvada. Väikese ja suure gravitatsioonilise läätse võimenduste kombineerumine loob võimaluse näha väga kaugele.

Ülikauge tähe avastamise võimaldas paljude juhuste kokkulangemine. Projekti esialgne eesmärk oli lihtsalt taevafoonil moonutusi tekitavate galaktikaparvede otsimine. Juhuslikult sattus aga ühe parve taga süttima supernoova. See viis galaktikaparve detailse uurimiseni. Ja selle uurimise käigus juhtusid ühele vaatekiirele sattuma kaks tähte eri galaktikates. Juhuste aheldumise tulemusena avastatigi Icarus.

Põhimõtteline võimalus näha nii sügavale ja seega ka ajas väga kaugele on pannud astronoomid otsima võimalusi selliste juhtumite süstemaatiliseks uurimiseks. Selleks aga, et nõela heinakuhjast leida, on vaja teha piisava sageduse ja lahutusvõimega üle taeva vaatlusi. Saadav andmevoog on väga suur, räägitakse isegi andmete tsunamist. XXI sajandi teleskoopide tööd mõõdetakse kümnetes terabaitides päeva kohta. Ainult väga võimsad arvutid suudavad neid andmeid töödelda ja saadud piltidelt huvitavaid nähtusi leida. Sealjuures peavad kasutatavad programmid olema piisavalt taibukad. Tehisintellekt, masinõpe, süvaõpe, närvivõrgud – kõik see ei ole astronoomide jaoks moodne sõnakõlksutamine, vaid igapäevane tegelik vajadus.

Neuronid ja tabelid

Üks esimesi tähti, mille vaatlused astronoomid sisestasid algandmetena tehisnärvivõrku (allpool lihtsalt võrku), oli eestlaste jaoks oluline täht Veega Lüüra tähtkujust. Muidugi võib siin ju vaielda, kas Veega kauguse leidnud baltisaksa astronoom Struve oli ikka eesti astronoom ja mis ühel talurahval kogu selle härrade tsirkusega üldse pistmist oli.

Seda teemat riivamisi uurides sattusin Herbert Ligi raamatu „Talupoegade koormised Eestis 13. sajandist 19. sajandi alguseni“ (Eesti Raamat, Tallinn 1968) peale. Sealt lugesin, et talurahva ajaloo uurimistes vajalikku statistikat tehes on kombeks talu veovõime arvutamisel lugeda üheks rakendiks üks hobune või paar härgi. Oletame, et see valem oli samasugune Struve-aegses imperiaalses statistikas. Seega, kui oli vaja talupoegade olukorra arvulist hindamist, tuli tabelist tabelisse sissekandeid tehes härgade arv korrutada 0,5 ga (kaaluga) ja liita sellele hobuste arv, kaugemates kubermangudes võisid oma kaaludega arvesse tulla ka kaamelid, eeslid jms. Kui juhtus nii, et järgmises tabelis ei olnud vaja arvesse võtta rakendite summaarset arvu, vaid piisavalt rakenditega varustatud talude arvu, siis pärast härgade, hobuste, kaamelite ja eeslite kaalutud liitmist võidi võrrelda saadud arvu mingi etteantud normatiivse väärtusega (näiteks 3). Kui summa oli normist suurem, siis läks talu hästi varustatute kirja.

Selliselt koostatud statistilised andmed (tabelid) liikusid mööda administratiivseid tasandeid ülespoole, jõudes vallast impeeriumi keskusesse ja lõpuks imperaatori endani. Igal tasemel liideti alumise taseme arvusid, korrutati neid vajaduse korral kaaludega, teisendati vajalikule kujule ja saadeti järgmisele tasemele.

Kui üldistatud andmed jõudsid imperaatorini, siis tema hindas kogu olukorda. Tulemusena hakkasid ülevalt alla liikuma ukaasid ja prikaasid, mis muu hulgas ja vajaduse korral sätestasid ka statistikas kasutatavate kaalude uued väärtused.

Kui nüüd seda lugu juhtub lugema infoinsener, siis on ta nägu juba ammu naerul ja ta taipab, kuhu sihin.

Võrkude elementaarseteks osakesteks on neuronid – lihtsad arvutuseeskirjad, kus liidetakse kaaludega läbi korrutatud sisendiks olevad arvud (ühega korrutatud hobuste arv pluss poolega (0,5) korrutatud härgade arv, siis eeslid jne) ja saadud summale rakendatakse sobilik teisendus (kui summa on suurem kui 3, siis on talu piisavalt varustatud). Oma nime on neuronid saanud rakkudelt, mis kontrollivad inimese või looma juhtimisprotsesse. See ajalooliselt kujunenud nimi võib olla natuke eksitav. Infoneuronil ja tavalisel neuronil on ainult niipalju ühist, et nad võtavad oma väljundi „arvutamisel“ arvesse mitut sisendit, millest igaühe panus on kontrollitud kaaludega (kaks härga, kolm eeslit jne).

Andmed ja parameetrid võrkudes on organiseeritud tabelitena (tensoritena, vastavalt eriala kõnepruugile). Eesti­pärasemalt kasutame aga allpool tensori kohta nimetust plokk. Võrkude kirjeldamiseks kasutatakse tihti diagramme, kus värvilised kastikujulised plokid on asetatud ridamisi, näitamaks algoritmi töö eri faase. Mulle tuletavad need plokid meelde plastiliinikarpe lapsepõlvest. Esialgu tähenduseta värvilisi plokke oli võimalik voolida mis tahes loomadeks või viguriteks. Täpselt nagu alguses juhuslikke arve sisaldavatest kaalude plokkidest saab õpetamise käigus „voolida“ kasulikke mälumooduleid.

Ülekanded ja arvutused ühest tabelist teise võivad toimuda kahes suunas. Alt üles liikumine on kirjeldatav neuronkihtide läbiarvutamisega (valla pudu­lojuste tabelist piisavat veojõudu omavate talude arvu tabelisse ja sealt edasi). Imperaatori tuju arvesse võttev allapoole suunatud tegevus – vajalike paranduste sisseviimine kaalude tabelitesse (tagasi­levi) on samuti suhteliselt lihtne mehhaaniline arvutusprotsess.

Õppida, õppida, õppida

On kaks võrgu „õpetamise“ võimalust. Juhendatud õppe puhul kasutatakse harimiseks treeningandmestikku, kus läbi võrgu lastakse andmeid, mille jaoks arvutuste vastus on juba ette teada. Esialgu on juhuslikult parametriseeritud võrk üsna abitu ja tema arvutatud tulemused kaugel õigetest. Kuid just see erinevus õige tulemuse ja arvutatu vahel annab vihje selle kohta, mida võiks paremini teha. Tagasilevi kaudu levib informatsioon vigade kohta allapoole (imperaatorist talumeheni) ja järgmise iteratsiooni jaoks kasutatakse juba täpsustatud parameetreid.

Juhendamata õppe puhul sisestatakse võrku suur hulk algandmete variante ja lastakse võrgul neid ise korrastada. Miks ja kuidas, sellest natuke hiljem.

Kui tehisnärvivõrk on treenitud (kaalude väärtused paika naelutatud), siis teda tihti veel testitakse ja lõpuks on ta valmis reaalseks tööks. Treenimine ja testimine on väga aja-, energia- ja rahamahukas toiming, võrgu kasutamine võib olla aga momentaalne ja suhteliselt odav.

Lihtne algus

Üks esimesi närvivõrkudel põhinevaid masinõpperakendusi astronoomias oli suurte, mitme peegliga teleskoopide juhtimine. Selleks et võimalikult teravat pilti saada, oli vaja peeglite asendeid pidevalt muuta. Juhtimiseks vajalike mehhaaniliste parandite suurused on väga keeruliselt seotud peeglite ees oleva õhumassi seisundi ja teleskoobi enda asendiga. Valemitega on neid seoseid väga raske kirjeldada ja sellepärast hakati kasutama tehisnärvivõrke. Heaks näiteks on kindlasti Mt. Hopkinsi mäe otsas olevas observatooriumis aastatel 1979–1998 töötanud kuue peegliga teleskoop MMT (Multiple Mirror Telescope). Juba 1990.–1991. aastal ilmusid ajakirjas Nature teedrajavad artiklid, kus kirjeldati detailselt kasutatud metoodikaid. Sealhulgas ka seda, millist rolli mängis Veega täht.

Kasutatud võrk ise oli väga väike ja lihtne, sisendiks 512 pikslist koosnev mustvalge pilt, väljundiks kümmekond numbrit. Sisendi ja väljundi vahel oli ainult üks, nn varjatud kiht neuroneid. Tehniliselt võiks öelda, et tegemist oli klassikalise pertseptron-arhitektuuriga.

Tänapäevased võrgud sisaldavad mitut varjatud vahekihti ja sellepärast on vastavat metoodikat hakatud nimetama võrkude süvaõppeks (ingl deep learning). Ettevaatamatusest võib aga siin tekkida mõtteseos sügava mõtlemisega …

Üks pilt on parem kui …

Võrkude peamiseks kasutusvaldkonnaks sai siiski pilditöötlus. Kõige esimeseks astronoomiliseks rakenduseks oli ülesanne eristada Palomari taevaülevaate plaatidelt skaneeritud piltidel galaktikad tähtedest.²

Alguses prooviti kasutada jälle kõige lihtsamat võrgu kolmekihilist arhitektuuri – sisendplokk, varjatud neuronite plokk, väljundplokk. Treenimiseks kasutati „näpuga näitamist“ ehk siis inimese läbiuuritud pilte, kus tähed, galaktikad ja müraplekid olid juba eristatud.

Üsna kiiresti õpiti aga kasutama keerukamaid võrke. Alguses lisati sisendi ja väljundi vahele rohkem neuronite kihte – plokke (süvaõpe). Kuna iga järgmises kihis asuva neuroni sisendiks olid kõik eelmise kihi neuronid, siis vajalike arvutuste maht kasvas väga kiiresti.

Siis aga võeti õppust mõnest inimese aju ehituse eripärast ja hakati kasutama sidumipõhiseid võrke. Just selliseid, sagedasti kasutatavaid võrke on mõistlik veidi üksikasjalikumalt kirjeldada.

Küllap on kõik näinud, kuidas vanemad inimesed loevad lehte või raamatut kasutades luupi. Seda väärtuslikku instrumenti liigutatakse alguses mööda teksti ülemist serva vasakult paremale, siis liigutatakse luup natuke allapoole ja vasakust äärest jälle paremale jne. Sidumi­põhises võrgus toimub kõik samamoodi. Suhteliselt väikest ruudukujulist kaaludeplokki liigutatakse nagu luupi sisendpildi suhtes ja igas peatuspunktis teostatakse hobused-härjad-eeslid-tehteid. Tulemused aga saadetakse uue pildina järgmises kihis töötlemiseks.

Iga selline „luubiga“ lugemine võimaldab eristada pildis erinevaid detaile. Mõni kaalude plokk on tundlik rõhtsete kriipsude suhtes, teised on tundlikud ristide suhtes jne. Mida iga plokk tegelikult arvutab, sõltub võrgu treenimisest, inimene siin midagi ette ei kirjuta.

Sidumipõhiste võrkude rakendamine oli kiirem ja andis ka paremaid tulemusi. Kui aga jõuti suuremate piltide töötlemiseni, jäid astronoomid hätta. Juhendatud õpe vajab juhendaja – inimese – osavõttu treeningprotsessist. Mida suurem mudel, seda suuremat kogust valmis sorditud andmeid peab treenimiseks kasutama. Aga kui palju neid üliõpilasi või Galaxy Zoo projektist osa võtvaid vabatahtlikke galaktikate uurijaid jätkub?

Seega, juhendatud õppe põhimõte ise seab piirid paljudele masinõppe rakendustele. Kas on mingi võimalus inimesest täiesti lahti saada ja lasta masinal kogu töö ära teha?

Loomadest veel, seekord ahvidest

Hästi on tuntud lugu ahvidest, keda on pandud arvutisse teksti sisse toksima, lootes, et nad kunagi ka terve teosega, nagu näiteks William Shakespeare’i „Hamletiga“ hakkama saavad. Matemaatikud väidavad, et see aeg saabub peaaegu kindlasti, kuskil igaviku piiril.³ Moraal seisneb selles, et huvitavad pildid, arvuread, tekstid jms moodustavad väga väikese osa kõikidest võimalikest pikslite, arvude ja tähtede kombinatsioonidest.

Juhendamata õppe mõte ongi hiigelsuure hulga võimaluste seast vajaliku alamhulga väljaeraldamine. Üks meetodeid, mis seda võimaldab, on autokodeerijatena töötavad võrgud.

Vajalik algoritm ise on imelihtne. Koostame võrgu skeemi, kus sisendi ja väljundi vahel on mitu neuronite vahekihti. Treenime võrku, sisestades sinna kõik oma pildid, täpsustamata, mis on pildil. Sihifunktsiooniks (imperaatori nõudeks) aga seame, et võrgu väljundpilt sarnaneks maksimaalselt sisendpildile.

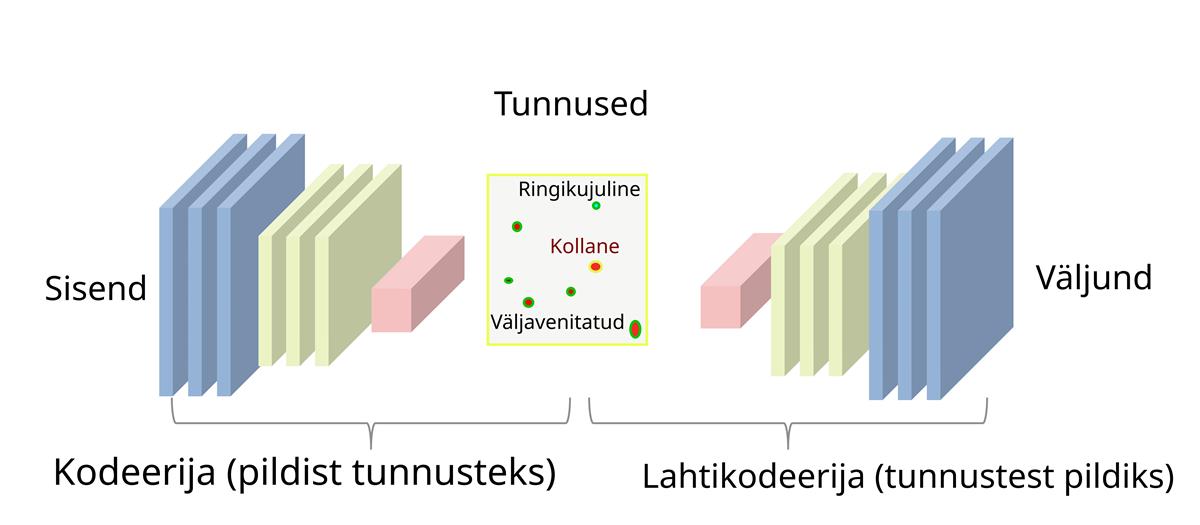
Lugeja saab kohe aru, et võimalik võrgu skeem on ju lihtne – laseme pildid otse sisendist väljundisse. Autokodeerijas käib asi aga veidi keerulisemalt. Ta projekteeritakse nii, et keskmistes kihtides on tunduvalt vähem neuroneid. Neid on nii vähe, et pigem pole tegemist enam moonutatud piltide, vaid hoopis tunnuste kogumiga. Kui inimene peaks sama tööd tegema, oleks seal sellised tunnused nagu „ringikujuline“, „kollane“, „väljavenitatud“ jne. Masinõppe varjatud kihtides olevad tunnused tekivad aga õppe käigus ja need ei ole otseselt seotud inimese leiutatud mõistetega.

Sisuliselt koosneb autokodeerija kolmest osast: kodeerijast, tunnuste kihist ja lahtikodeerijast. Autokodeerijas treenitud võrku saab mitmel eri moel rakendada.

Astronoomias kasutatakse seda skeemi objektide klassifitseerimiseks. Oletame, et meil on vaja sorteerida piltidel olevad udused laigud tähtedeks, lihtsateks galaktikateks, interakteeruvateks galaktikateks ja läätsefekti poolt moonutatud galaktikateks. Selleks laseme autokodeerijast läbi kõik oma seni pildistatud taevakujutised, olgu neid või paarsada tuhat. Imperaatori käsuks on: „Mis sisse läheb, peab välja tulema.“ Külmutame nüüd paika õpitud kaalude väärtused ja viskame arvutuskeemist välja lahtikodeerija osa. Tulemuseks on meil arvutusmoodul, mis võimaldab suvalise sisendpildi teisendada väikeseks tunnuste hulgaks.

Kui nüüd sellele moodulile lisada veel mõned neuronite kihid koos oma parameetritega ja anda neile täpsustavat õpet, saame vajaliku klassifikaatori. Õpetamise sihifuktsiooniks oleks siis võrgu arvutatud objekti klassi ja inimese antud klassifikatsiooni kokku­langemine. Kuna lisatud kihtide sisendiks on väike hulk tunnuseid, siis on juhendatud täiendõppeks vaja tunduvalt vähem näitepilte.

Autokodeerijat võib kasutada ka üldse ilma täpsustavalt õpetamata. Näiteks võiks tuua Tõravere astronoomide lemmikandmebaasist SDSS (Sloan Digital Sky Survey) anomaalse spektriga galaktikate otsimise.⁴

Valmis treenitud autokodeerija lahti­kodeerijat (tunnustest pildi arvutajat) võib kasutada aga uute pildivariantide genereerimiseks. Küsige oma laste või lastelaste käest, nad näitavad teile, kuidas generatiivsete närvivõrkude abil saab Obamast Trumpi teha või vastupidi.

Vanad joonistused

Pilte töötlevate võrkude õpetamiseks kasutatakse tihti kahe eri „huvidega“ võrgu koostööd. Oletame, et meie imperaator on kogunud hulga Madalmaadest kalli raha eest ostetud maale. Et oma galerii laiendamiseks raha kokku hoida, annab ta õuekunstnikule ülesande maalida võimalikult sarnaseid pilte. Iga valmis maalitud pilti näitab kunstnik nüüd imperaatorile, kes peab otsustama, kas tehtud pilt on „tõeline“ või mitte. Maalija sihifunktsiooniks on suur korralike võltsingute arv. Imperaatori mudelit treenitakse aga talle nii õuekunstniku kui ka Madalmaadest toodud originaale näidates. Tema võrgu parameetreid tuunitakse vastavalt sellele, kui täpselt ta kahte tüüpi eristada oskab.

See, nn generatiivsete vastastikuste närvivõrkude meetod on leidnud kasutust mitmes astronoomilises projektis. Toreda näitena võib tuua töö,⁵ kus Galileo päikeseplekkide joonistuste põhjal arvutati välja, kuidas tollane päike võis välja näha, kui teda oleks vaadeldud tänapäeva vaatlusriistadega.

Vaatame, mis tuleb

Kui tahame tuleviku taevaülevaadetest kätte saada kõike, mis huvitav, peame uurima, kuidas vaadeldud ja süvaõppe poolt eristatud objektide heledus ajas muutub.

Piltide puhul sisestame võrku fikseeritud mõõtmetega pilte. Aegridadega on aga asi hullem. Erinevate vaatlusridade pikkus (vaatluspunktide arv reas) on muutuv. Selliste andmete töötlemiseks sisestatakse neuronitest koosnevatesse skeemidesse andmeid üks punkt korraga. Esimene vaatlus, siis teine jne. Rekurrentsete närvivõrkude meetodiks kutsutud arvutusskeeme kasutavad astronoomid päikeseplekkide, muutlike tähtede, supernoovade, mikroläätse efekti, eksoplaneetide, kiirete raadiosähvatuste jms uurimiseks. Erinevate muutuste klassifitseerimise kõrval on võrgud kasulikud ka tulevikus toimuvate sündmuste ennustamiseks.

Astronoomid ja revolutsioon

Harva, kui revolutsiooni algus on nii hästi dokumenteeritud nagu praegune tehisintellektiga seotu. Nimelt, 2017. aasta suvel ilmus tagasihoidlik preprint ja hiljem lõpuni toimetatud artikkel peakirjaga „Tähelepanu on kõik, mida vajad“.⁶ Artiklis kirjeldati uut masintõlkeks loodud närvivõrkude kasutamise skeemi, millele pakuti nimeks „transformaator“.

Viis aastat hiljem, 30. novembril 2022, teatas USA väike kompanii OpenAI, et nad on tarvitamiskõlblikuks saanud juturoboti ChatGPT (Chat Generative Pre-training Transformer), mis lähenes nn Turingi lävele – inimene ei osanud tihti enam vahet teha, kas temaga räägib robot või teine inimene. Kõik järgnev on teada ja tuntud ja sellel pole mõtet peatuda. Kasutame parem juhust ja tarvitame ülaltoodud mõisteid ja näiteid revolutsioonilise tarkvara ligikaudseks kirjeldamiseks.

Kuna inimene loeb teksti sõnade kaupa, siis traditsioonilistes keelemudelites kasutati rekurrentseid närvivõrke, sisendiks ikka üks sõna korraga, täpselt nii nagu muutlike tähtede uurimisel (seal siis ikka üksiku vaatluse kaupa). Revolutsioonilise transformaatori puhul aga teisendatakse tekst alguses kujundlikult öeldes piltideks. Kui astronoomilist värvipilti võib kirjeldada kui teatud laiuse, kõrguse ja sügavusega (värv) arvude plokki, siis transformaatorisse sisestatakse fikseeritud laiuse ja kõrgusega kahemõõtmelisi „pilte“. Vastava ploki elemendid arvutatakse aga õppematerjaliks olevate tekstide fragmente kasutades.

Kui astronoomilises pilditöötluses kasutatakse sidumipõhiseid arvutuskihte, siis transformaatorites on olulised samuti lihtsad, kuid mõnevõrra erinevad arvutused. Mingi ettekujutuse võime saada, kui kujutame ette, et tekstipilte vaadeldakse mitte ühe luubiga, vaid kahe luubiga. Kui ühe luubi vaateväljas on sõna „kass“ ja teise luubi vaateväljas on sõna „kollane“, siis kassi kirjeldavas andmereas võidakse anda sõnale „kollane“ suurem kaal, s.t osutatakse sellele sõnale tähelepanu. Transformaatorile peab muidugi õigeid raamatuid näitama, eriti Mati Undi teoseid.

Transformaatori õpetamine (eeltreening) toimub ilma juhendamiseta. Nagu autokodeerijates üldiselt, on eesmärgiks see, et sisendtekst ja väljundtekst kokku langeksid. Seda küll erilisel moel – järgmist sõna ennustades, samm-sammult.

Juturoboti ChatGPT puhul kasutati transformaatorit eeltreeninguks ja selle järel juhendatud õpetamist järeltreenimiseks, täpselt nagu astronoomilises klassifitseerimisülesandes. Kuna eel­treeningu käigus on kogu treeningmaterjal pakitud suhteliselt väikestesse tähelepanu­plokkidesse, siis pole järeltreeningu seansse väga palju vaja. ChatGPT keelemudeli GPT-3 esialgses versioonis kestis eeltreening mitu kuud ja tulemusena häälestati 175 miljardit parameetrit-kaalu (mitu hobust-härga jne). Järeltreeningu kohta palju andmeid ei ole.

Transformaatorid ja tähelepanu mehhanism on leidnud juba otsest kasutust astronoomias. Esimesed tööd on ilmunud nende rakenduste kohta kiirete üleminekute (plahvatused jms) detekteerimisel ja samuti pilditöötluses – gravitatsioonilises läätses lõhestatud ja moonutatud kujutiste otsimisel.

Millist kasu võiksid astronoomid veel saada keset praegust tehisintellekti ja masinõppe ümber kohisevat revolutsioonilist melu?

Võib-olla kõige tähtsam on eeldatav kiire numbriliste protsessorite tootmise kasv, nende võimekuse suurenemine, turu laienemise ja konkurentsi tõttu ka odavnemine. Plokiprotsessorid on praegu üsna kallid, näiteks NVIDIA A100 protsessor (selliseid kasutatakse juturobotite treenimiseks) maksab 6000 – 15 000 dollarit. Aga vaja võib neid minna palju, näiteks GPT-keelemudeli treenimisel kasutati neid hinnanguliselt 30 000 tükki.

Kindlasti on kasu ka uutest rahavoogudest, mis toetavad tehisintellekti, masinõppe ja eriti süvaõppega seotud uurimisi. Astronoomid on ju alati olnud esimeste uute tehnoloogiate rakendajate hulgas. Näiteks juba 1976. aastal alustasid insener Jim Janesick ja planeetide uurija Brad Smith taevavaatlusi, kasutades pildi registreerimiseks ränisensoreid. Nüüd on iga inimese telefonis neid juba päris mitu.

Mida kiiremini astronoomid omandavad uued masinõppe tehnoloogiad, seda kaugemale ja detailsemalt hakkab inimene koos masinatega maailmaruumi nägema. Ja võib-olla ongi see nende olemise sügavam mõte. Ilma imetlejateta oleks universum täiesti mõttetu.

1 Jaan Pelt, Uued augud plekist taevas ehk kosmilised korduslinastused. – Sirp 19. VIII 2022.

2 S. C. Odewahn, E. B. Stockwell, et al., Automated Star/Galaxy Discrimination With Neural Networks. – The Astronomical Journal 1992, 103, lk 318–331.

3 Infinite monkey theorem, Wikipedia.

4 Vanessa Böhm, Alex Kim, Stéphanie Juneau, Fast and efficient identification of anomalous galaxy spectra with neural density estimation. Preprint arXiv:2308.00752v, 1. VIII 2023.

5 Harim Lee, Eunsu Park, Yong-Jae Moon, Generation of Modern Satellite Data from Galileo Sunspot Drawings in 1612 by Deep Learning. – The Astrophysical Journal 2021, v907, n2.

6 Ashish Vaswani, Noam Shazeer et al., Attention is All you Need. NIPS’17: Proceedings of the 31st International Conference on Neural Information Processing Systems 2017, lk 6000–6010.